나온지 꽤 된 논문인데요, ML 도메인에서는 아주아주 유명한 논문인 것 같습니다. ILSVRC'15 에서 당당하게 1위를 차지한 모델로, CVPR'16의 best paper 로 선정되었습니다. 마이크로소프트 북경 연구소에서 개발하였고, ResNet 으로 불리는 네트워크입니다. Shortcut/Skip connection 을 이용하여 residual (잔차) 을 학습시켜 성능을 향상시킨 논문으로, 이후 대부분의 모델들에서 ResNet 을 활용하게 되었습니다.
Inspiration
이 논문이 발표되기 이전까지, CNN 기반 모델의 정확도를 높이기 위해서는 보다 깊은 네트워크를 구성해야한다고 생각했습니다. 실제로 당시의 논문들을 보면 보다 깊은 네트워크의 성능이 더 나은 경우가 많았습니다.
이러한 가정으로부터 다음과 같은 질문이 떠오릅니다.
네트워크를 더 깊게 하면 성능이 더 좋아질까?
우선 직관적으로 떠올릴 수 있는 문제가 있습니다. 네트워크가 깊어질수록 점점 gradient 가 콩알만큼 작아지거나 반대로 폭탄만큼 커지는 vanishing/exploding gradient 문제가 발생합니다. 그렇지만 이 문제점에 대한 해결책으로 normalized initialization, intermediate normalization layers 등이 제안되었습니다.
Inception 과 VGG 등의 모델이 깊은 네트워크여서 성능이 좋았다고 말하기도 했는데, 위의 의문에는 Yes 라고 답할 수 있을까요? 정답은 No 였습니다. 왜 정답이 No 인지에 대해 알기 위해 우선 얕은 (Shallower) 네트워크에 레이어를 추가하는 것을 생각해봅시다. 이때 뒤에 추가하는 레이어는 convolution 하지 않고 값을 전달하는, 간단하게는 덧셈 연산과 같은 identity mapping 이라고 가정합니다. 깊어진 네트워크는 이론적으로 더 높은 에러를 내면 안됩니다.

저자들은 이것에 대해 답하기 위한 실험을 했고, 결과는 위의 그림과 같았습니다. 네트워크의 뒤에 층을 더 쌓았더니 오히려 성능이 떨어졌습니다. Training, test error 모두 높아진 것으로 보아 이는 overfitting 의 문제가 아닙니다. 이에 대해 네트워크가 깊어질수록 최적의 정답을 찾기가 어렵다, 즉 optimization 이 어렵다는 것을 원인으로 꼽았습니다. 얼추 무슨 근거로 정답이 No 인지를 확인했으니, 이제 깊은 네트워크가 성능이 좋아질 수 있는 모델을 만들 수 있는 방법에 대해 논문에서 답을 찾아보겠습니다.
Shortcut Connections
깊어진 네트워크는 optimization 이 어려워지는 문제점이 있습니다. 여기서 저자들은 한가지 가설을 세웁니다.
쌓인 레이어들의 underlying mapping 을 최적화 하는 것보다,
residual mapping 을 최적화하는 것이 더 쉬울 것이다.
이 가설을 풀어서 쓰면 다음과 같습니다.
- 보통 신경망을 이용할때는 $H(x)=y$ 를 만족하는 $H(x)$ 를 찾는것을 목표로 함
- 최적화를 통해 $H(x)-y$ 의 값을 최소화해나가며 $H(x)$ 를 찾아나감
- Identity mapping 함수에서는 $H(x)-x=0$, 즉 $H(x)=x$ 를 목표로 함
- 반면 ResNet 에서는 이를 $H(x)-x=F(x)$ 로 두고 $F(x)$ 를 최소화하는 것을 목표로 최적화를 함
- 이렇게 하면 $F(x)=0$ 이라는 목표가 생기기 때문에 기존보다 최적화가 더 쉬울 것임
즉 저자들은 쌓인 네트워크에서의 $x$ 라는 값에 매핑하기 위한 함수를 찾는 것보다, 0 에 맞추는 것이 훨씬 쉽지 않을까 라고 이야기 하는 것입니다. 위 식은 $H(x)=F(x)+x$ 로 나타낼 수 있고, 이는 "shortcut connections" 를 지닌 feedforward network 라고 할 수 있습니다.
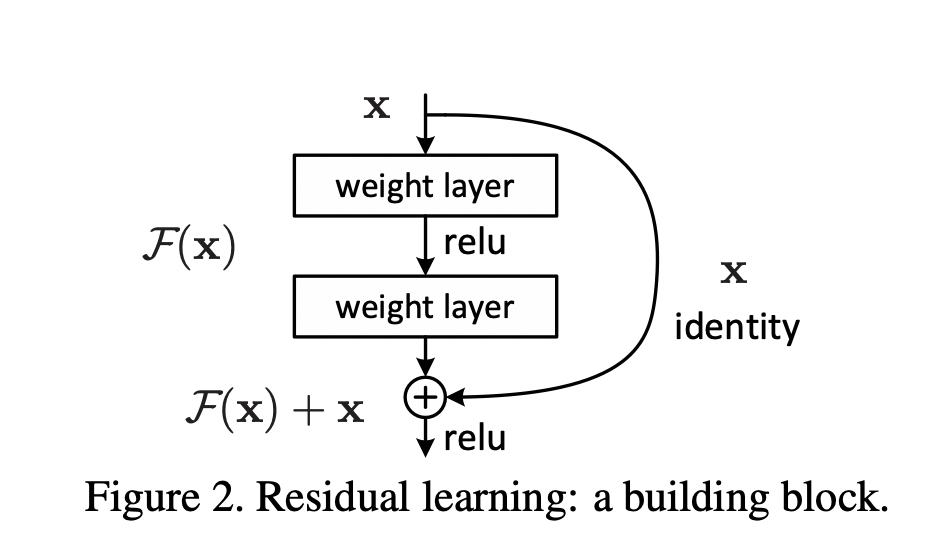
Training Residual Networks
Residual Networks 에서 사용되는 수식은 다음과 같습니다.
$$
\begin{align}
\mathbf y &= F(\mathbf x, {W_i})+\mathbf x \\
\mathbf y &= F(\mathbf x, {W_i})+W_s \mathbf x \\
\end{align}
$$
$F(\mathbf x, {W_i})$ 는 학습해야할 residual mapping 입니다. $F$ 와 $\mathbf x$ 의 차원은 동일해야하는데, 만약 그렇지 않다면 linear projection $W_s$ 를 활용해서 차원을 맞춰줄 수 있습니다 (논문에서는 $W_s$ 에 행렬을 사용해도 되지만, identity mapping 으로 충분하다는 사실을 실험들을 통해 밝혔습니다). 또한 $F$ 의 형태는 매우 자유롭지만, single layer 의 경우에는 $y=W_1 \mathbf x + \mathbf x$ 와 같은 형태의 linear layer 가 되어버려 아무 이점이 없습니다.
ImageNet 데이터셋을 활용해서 학습시킨 결과는 다음과 같습니다. Plain network 에서 residual networks 를 추가한 결과입니다. Plain networks 에서는 앞서 살펴본 것과 같이, 34-layer 의 경우가 성능이 더 떨어진 반면, ResNet 에서는 네트워크가 깊어질 수록 성능이 더욱 높아진 것을 확인할 수 있습니다.

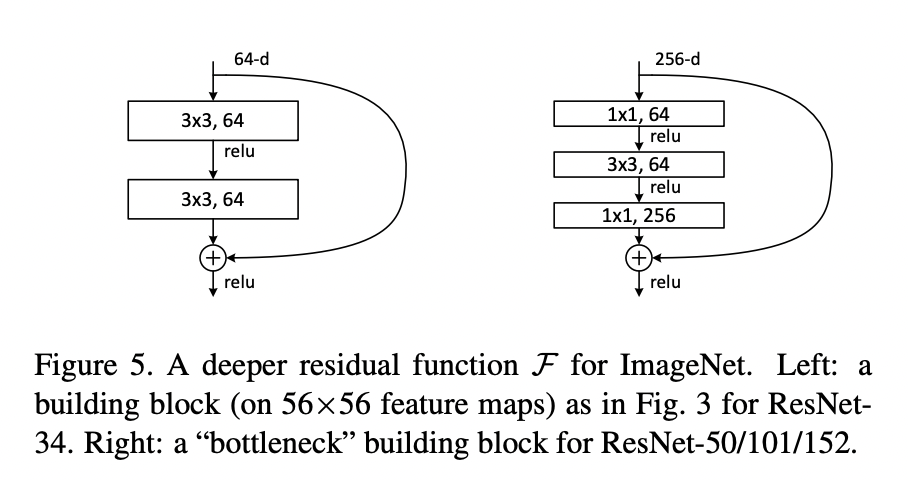
저자들은 이에 더해, 보다 깊은 네트워크에서의 실용적인 기법으로, Bottleneck 구조를 활용했습니다. 아래 그림의 왼쪽과 같이 3x3 의 convolutional layer 2개로 구성되었던 residual block 에서, 1x1, 3x3, 1x1 의 convolutional layer 로 구성하였습니다. 이렇게 변경함으로써 파라미터의 개수가 감소하여 연산량이 적어지는 장점이 있습니다.
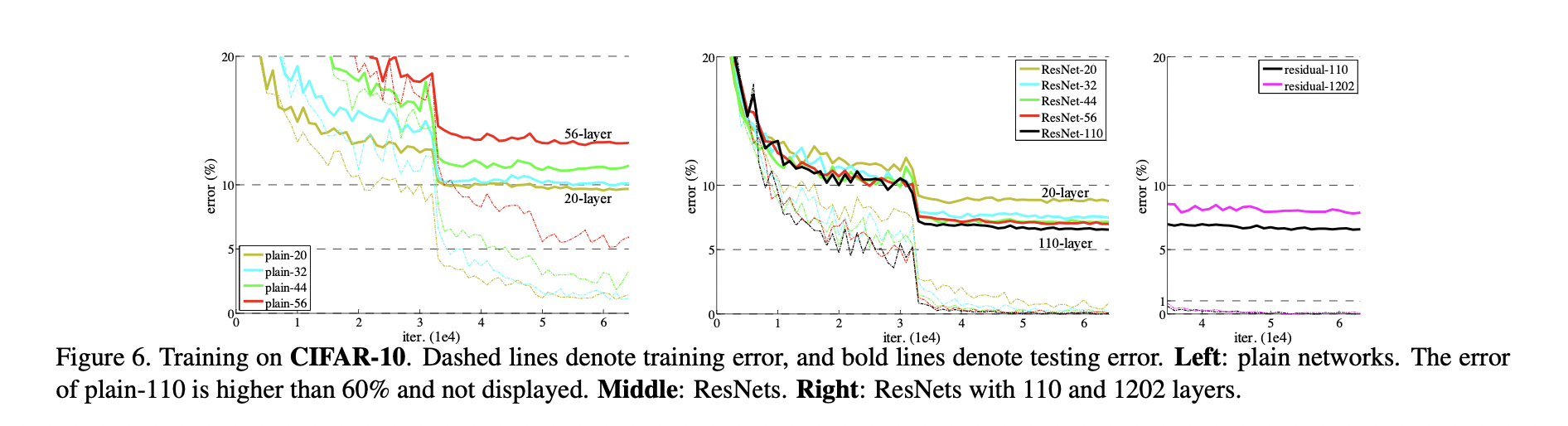
CIFAR-10 데이터셋을 활용해서 다양한 구성의 ResNet 을 실험한 결과, 110 개의 층을 사용한 모델이 가장 성능이 높았고, 1202 개의 층을 사용했을때는 overfitting 이 발생했습니다.
'development' 카테고리의 다른 글
| [CUDA] Triton kernel linking, with CUDA C++ (0) | 2025.07.05 |
|---|---|
| [CUDA] Pageable vs. Pinned Data Transfer (0) | 2025.06.19 |
| [CUDA] Shared memory: Bank Conflicts (0) | 2024.12.02 |
| [CUDA] GPU는 어떻게 빠른 연산이 가능할까? (0) | 2024.09.10 |
| [ML] CNN의 Translation Invariance에 대하여 (1) | 2024.08.14 |